Prime Number Checker in C#
Welcome to the Prime Number Checker Program in C# course! In this lesson, we will delve into the fascinating world of prime numbers and explore how to create a program that checks whether a given number is prime or not.
Introduction to Prime Numbers
Table of Contents
At its core, a prime number is a natural number greater than 1 that is divisible only by 1 and itself. In other words, a prime number cannot be evenly divided by any other number except for 1 and itself.
Definition of Prime Numbers
A more formal definition of prime numbers is that they are positive integers with exactly two distinct positive divisors: 1 and the number itself. For example, 2, 3, 5, and 7 are prime numbers since they can only be divided by 1 and themselves without any remainder. On the other hand, numbers like 4, 6, 8, and 9 are not prime since they have divisors other than 1 and themselves.
Properties of Prime Numbers
Prime numbers possess several interesting properties that make them unique and important in mathematics and computer science. Some of these properties include:
- Prime Factorization: Every positive integer can be expressed as a unique product of prime numbers. This property is known as prime factorization and is the foundation of many number theory concepts.
- Sieve of Eratosthenes: This ancient algorithm helps to identify all prime numbers up to a given limit efficiently.
Understanding the Problem
Before we dive into coding the Prime Number Checker program, it’s important to break down the problem statement and identify the requirements and constraints.
Break Down the Problem Statement
The problem statement is simple: we need to create a method that checks if a given number is prime. The method should take a number as input, perform the prime number check, and return a boolean value indicating whether the number is prime or not.
Identify the Requirements and Constraints
To solve this problem, we need to consider the following requirements and constraints:
- The program should prompt the user to enter a number for prime number checking.
- The program should call the prime number checking method and display whether the number is prime or not.
- The prime number checking method should determine if the given number is prime based on the definition and properties of prime numbers.
Objectives
The objectives of understanding, learning, practicing, and applying are essential when it comes to programming. These objectives help individuals develop their skills and knowledge in a structured and effective manner. By following these objectives, programmers can enhance their understanding of programming concepts, learn new techniques and best practices, practice their skills through hands-on exercises, and apply their knowledge to real-world scenarios. This approach ensures a comprehensive and well-rounded learning experience.
Objective 1: Understand
The first objective is to understand the concept of prime numbers and how to check whether a number is prime or not. A prime number is a number greater than 1 that can only be divided by 1 and itself without leaving a remainder. For example, 2, 3, 5, 7, 11, and 13 are prime numbers. Understanding the properties and characteristics of prime numbers is crucial for implementing a prime number checker program.
Objective 2: Learn
The second objective is to learn the programming language and syntax required to implement a prime number checker program. In this case, we will focus on C#. Learning the fundamentals of C# programming, including variables, loops, conditionals, and functions, will enable us to write a program that can determine whether a given number is prime or not.
Objective 3: Practice
The third objective is to practice implementing a prime number checker program in C#. Through practice, we can reinforce our understanding of the programming concepts and syntax learned in Objective 2. By writing code, running it, and debugging any errors or issues that arise, we can improve our programming skills and gain confidence in our ability to solve problems using C#.
Objective 4: Apply
The fourth objective is to apply the knowledge and skills gained from understanding, learning, and practicing to create a functional prime number checker program. By applying our knowledge, we can develop a program that takes a user-inputted number and determines whether it is prime or not. This program will utilize the concepts and techniques learned in Objectives 1-3 to provide an accurate result.
Source code example
using System;
namespace PrimeNumberCheckerApp
{
public class PrimeNumberChecker
{
public static bool IsPrime(int number)
{
if (number <= 1)
{
return false;
}
for (int i = 2; i <= Math.Sqrt(number); i++)
{
if (number % i == 0)
{
return false;
}
}
return true;
}
public static void Main(string[] args)
{
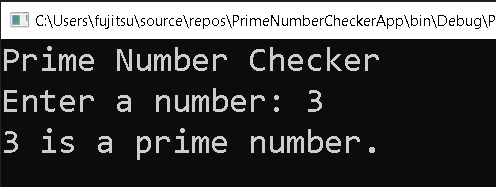
Console.WriteLine("Prime Number Checker");
Console.Write("Enter a number: ");
int number = Convert.ToInt32(Console.ReadLine());
if (IsPrime(number))
{
Console.WriteLine($"{number} is a prime number.");
}
else
{
Console.WriteLine($"{number} is not a prime number.");
}
Console.ReadKey();
}
}
}

Explanation
Here’s a breakdown of the C# code for a prime number checker, explained for beginners:
- Getting Started:
- using System;: This line imports the System namespace, which contains essential tools like Console for input/output and Math for mathematical functions.
- Creating the Checker Class:
- namespace PrimeNumberCheckerApp: This creates a namespace to organize the code.
- public class PrimeNumberChecker: This defines a class named PrimeNumberChecker, which will hold the code for checking prime numbers.
- Checking for Primes:
- public static bool IsPrime(int number): This method takes an integer (number) and returns a boolean value (true if prime, false if not).
- if (number <= 1): This checks if the number is less than or equal to 1, which are not prime, and returns false.
- for (int i = 2; i <= Math.Sqrt(number); i++): This loop starts from 2 and goes up to the square root of the number, checking for potential divisors.
- if (number % i == 0): If any divisor is found (number is divisible by i), it means it’s not prime, so return false.
- return true;: If no divisors are found within the loop, the number is prime, so return true.
- Running the Program:
- public static void Main(string[] args): This is the entry point of the program, where execution begins.
- Console.WriteLine(“Prime Number Checker”);: Prints a welcome message to the console.
- Console.Write(“Enter a number: “);: Prompts the user to enter a number.
- int number = Convert.ToInt32(Console.ReadLine());: Reads the input number and converts it to an integer.
- if (IsPrime(number)): Calls the IsPrime method to check if the entered number is prime.
- Console.WriteLine($”{number} is a prime number.”);: Prints a message indicating the number is prime.
- else: If the number is not prime, prints a message stating it’s not prime.
Output
Summary
In this lesson, we covered the concept of a prime number and implemented a prime number checker program in C#. The objectives of understanding, learning, practicing, and applying were followed to ensure a comprehensive learning experience.
We started by understanding that a prime number is a number greater than 1 that can only be divided by 1 and itself without leaving a remainder. This understanding helped us implement a prime number checker program effectively.
Next, we learned the C# programming language and syntax required to implement the program. We focused on fundamental concepts such as variables, loops, conditionals, and functions.
We then practiced our programming skills by writing code, running it, and debugging any issues that arose. Through practice, we reinforced our understanding of the programming concepts and improved our overall skills.
Finally, we applied our knowledge and skills to create a functional prime number checker program. The program prompts the user to enter a number, calls the IsPrime method to check if the number is prime or not, and displays the result to the user.
By following these objectives and completing this lesson, we have gained a solid understanding of prime numbers, learned how to implement a prime number checker program in C#, practiced our programming skills, and successfully applied our knowledge to solve a real-world problem.
Keep practicing and applying your programming skills to continue building your expertise in C# and other programming languages.
Exercises and Assessment
- Optimize the prime number checking algorithm: The current implementation checks divisibility up to the square root of the number. However, you can further optimize the algorithm by only checking divisibility up to the square root of the number plus one, and incrementing the loop variable by 2 instead of 1. This is because all prime numbers greater than 2 are odd, so there’s no need to check even numbers.
- Handle input validation: Currently, the program assumes that the user will always enter a valid integer. You can improve the source code by adding input validation to handle cases where the user enters invalid input, such as non-numeric characters. You can use the int.TryParse method to validate the user’s input.
- Add exception handling: The current implementation doesn’t handle exceptions that may occur during input conversion or other operations. You can enhance the source code by adding exception handling to catch and handle any potential exceptions. For example, you can catch FormatException if the user enters non-numeric characters.
- Implement a prime number generator: Extend the program by implementing a method that generates a list of prime numbers up to a given limit. You can modify the IsPrime method to return a List<int> containing all prime numbers within the specified range. Then, modify the Main method to prompt the user for a limit and display the list of prime numbers.
These exercises will challenge you to think critically, improve your coding skills, and enhance the functionality of the source code. Happy coding!
Related Topics and Articles:
Random Number Generator in CSharp
Methods in C# Video Tutorial and Source code
You may visit our Facebook page for more information, inquiries, and comments. Please subscribe also to our YouTube Channel to receive free capstone projects resources and computer programming tutorials.
Hire our team to do the project.